6962. Батарея Бони
Бони исследует, какой электрический заряд батареи будет
наиболее подходящим для транспортных средств школьного округа его мамы. Каждая
школа имеет зарядную станцию. Поездка из одной школы в любую другую должна
происходить с не более чем k
подзарядками. Батарея автомобиля изначально имеет нулевой заряд и должна быть
пополнена в начале каждой поездки; это считается одной из k подзарядок. Существует не более
одной дороги между каждой парой школ, а также существует по крайней мере один
путь, соединяющий каждую пару школ. Одной единицы заряда достаточно чтобы
преодолеть одну единицу расстояния.
Зная расположение дорог и значение k, вычислить необходимый заряд электрической батареи транспортных
средств.
Вход. Начинается с количества тестов t (1 ≤ t ≤ 50).
Каждый тест начинается со строки, содержащей три целых числа n, k и m (2 ≤ n ≤ 100, 1 ≤ k ≤ 100), где n – количество школ, k – количество подзарядок, допустимых во
время путешествия, m – количество
дорог. Каждая из следующих m строк
содержит три числа ui, vi и di (0 ≤ ui,
vi < n, ui
≠ vi, 1 ≤ di ≤ 109)
указывающих на то что дорога i соединяет
школы ui и vi (0-индексируемые)
двусторонней дорогой с расстоянием di.
Выход. Для каждого теста вывести в отдельной строке наименьший
возможный заряд электрической батареи.
|
Пример
входа |
Пример
выхода |
|
2 4 2 4 0 1 100 1 2 200 2 3 300 3 0 400 10 2 15 0 1 113 1 2 314 2 3 271 3 4 141 4 0 173 5 7 235 7 9 979 9 6 402 6 8 431 8 5 462 0 5 411 1 6 855 2 7 921 3 8 355 4 9 113 |
300 688 |
РЕШЕНИЕ
Флойд-Уоршел
+ бинарный поиск
Анализ алгоритма
Наименьший возможный заряд электрической батареи ищем
бинарным поиском. Построим матрицу кратчайших расстояний dist между городами
при помощи алгоритма Флойда – Уоршела. Пусть аккумулятор имеет емкость mid. Определим, можно ли на нем проехать
из любого города в любой. Для этого создадим матрицу red, в которой положим red[i][j] = 1 если на одном заряде аккумулятора
можно добраться из i в j, и red[i][j] = ∞ иначе.
Запустим на ней алгоритм Флойда – Уоршела. Теперь red[i][j] содержит наименьшее
количество подзарядок, требуемых для проезда из i в j по оптимальному
маршруту. Найдем наибольшее значение len
в массиве red. Если len ≤ k, то при помощи аккумулятора емкости mid можно добраться из любого города в
любой совершив не более k подзарядок.
Пример
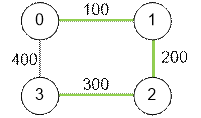
Для первого
примера наименьший возможный заряд электрической батареи равен 300. За одну
подзарядку из вершины 0 можно добраться в 2, за вторую подзарядку – из 2 в 3.
Реализация
алгоритма
Определим
константу бесконечность.
#define INF 0x3F3F3F3F3F3F3F3FLL
Расстояния дорог храним в массиве dist. Массив red используем
для дополнительных операций.
long long
dist[MAX][MAX], red[MAX][MAX];
При помощи
Флойда – Уоршела пересчитаем кратчайшие расстояния между городами.
void floydDist(void)
{
int i, j, k;
for (i = 0; i
< n; i++) dist[i][i] = 0;
for (k = 0; k
< n; k++)
for (i = 0;
i < n; i++)
for (j =
0; j < n; j++)
if
(dist[i][j] > dist[i][k] + dist[k][j])
dist[i][j] = dist[i][k] + dist[k][j];
}
При помощи
Флойда – Уоршела пересчитаем кратчайшие расстояния для матрицы red.
void floydRed(void)
{
int i, j, k;
for (i = 0; i
< n; i++) red[i][i] = 0;
for (k = 0; k
< n; k++)
for (i = 0;
i < n; i++)
for (j = 0; j < n; j++)
if
(red[i][j] > red[i][k] + red[k][j])
red[i][j] = red[i][k] + red[k][j];
}
Основная часть
программы. Читаем входные данные. Строим матрицу расстояний dist между
городами.
scanf("%d",&tests);
while(tests--)
{
scanf("%d %d %d",&n,&k,&m);
memset(dist,0x3F,sizeof(dist));
for (i = 0; i
< m; i++)
{
scanf("%d
%d %d",&u,&v,&d);
dist[u][v] = dist[v][u] = d;
}
Вычисляем кратчайшие расстояния между городами.
floydDist();
Искомый заряд электрической батареи ans ищем бинарным поиском. Изначально ans Î [1; ∞].
min = 1; max = INF;
ans = max;
while (min
<= max)
{
mid = (min + max) / 2;
Проверяем, можно ли добраться из любой школы в любую при
помощи батареи с зарядом mid.
Заполняем массив red таким образом что red[i][j] = 1 если на одном заряде аккумулятора
можно добраться из i в j, и red[i][j] = ∞ иначе.
for (i = 0;
i < n; i++)
for (j =
0; j < n; j++)
red[i][j] = dist[i][j] <= mid ? 1 :
INF;
Пересчитываем массив кратчайших расстояний для матрицы red.
floydRed();
Ищем максимальное значение len в матрице red. Оно равно количеству подзарядок батареи, необходимых
для преодоления максимального расстояния между парой городов.
len = 0;
for (i = 0;
i < n; i++)
for (j =
0; j < n; j++)
if
(red[i][j] > len) len = red[i][j];
В зависимости от значений len
и количества допустимых подзарядок k
изменяем интервал бинарного поиска.
if (len
<= k)
{
ans = mid;
max = mid - 1;
} else
min = mid + 1;
}
Выводим ответ.
printf("%lld\n",ans);
}